历史

1824年，在伦敦发行的《机械杂志》内的一副刻画。阿基米德说：“给我一个支点，我就可以撬起整个地球。”

早在旧石器时代晚期，古人就知道使用杠杆的原理来制作投枪器。 考古学者认为，在古埃及4500多年前的金字塔时期，工人使用杠杆来移动、抬举重量超过100英吨的方尖碑。 中国战国时期，墨子在所著作的《墨子》一书中，提到应用杠杆的概念。

大约在公元前330年，亚里斯多德在著作《机械问题》（《Mechanical Problems》）里，对于杠杆有详细的论述，并且基本而言使用虚功的现代概念推导出杠杆原理。 公元前3世纪，古希腊科学家阿基米德在著作《 论平面图形的平衡 》里用几何方法推导出杠杆原理， 并且宣称：“给我一个支点，我就可以撬动整个地球。”

概述

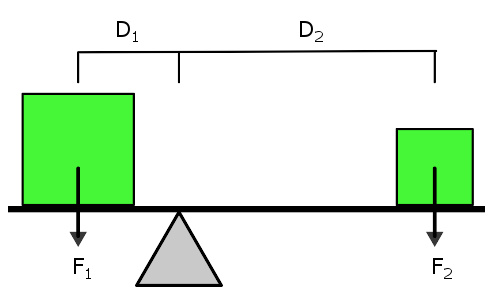
静力平衡的杠杆。

由于杠杆内部有一点为固定点，杠杆只能绕着这固定点做旋转运动。相对于这一点，杠杆不能做平移运动。

杠杆内部的固定点称为“支点”。

使杠杆旋转的力 F 1 {\displaystyle F_{1}} 叫做“动力”，是输入力。

动力作用于杠杆的位置叫做“动力点”。

阻碍杠杆旋转的力 F 2 {\displaystyle F_{2}} 叫做“阻力”，是输出力。

阻力作用于杠杆的位置叫做“阻力点”。

从支点到动力作用线的垂直距离 D 1 {\displaystyle D_{1}} 叫做“动力臂”。

从支点到阻力作用线的垂直距离 D 2 {\displaystyle D_{2}} 叫做“阻力臂”。

理想杠杆不会耗散或储存能量，也就是说，支点与硬棒之间不会出现任何摩擦损耗，硬棒是一种刚体，不会被弯曲，发生形变。注意到硬棒不一定是直棒。弯曲的硬棒形成的杠杆称为“曲杠杆”。对于理想杠杆案例，输入杠杆的功率等于杠杆输出的功率。输出力与输入力之间的比率，等于这两个作用力分别与支点之间垂直距离的反比率，称这相等式为“杠杆原理”，以方程表达：

或者，

定义力矩 M {\displaystyle M} 为

其中， F {\displaystyle F} 是作用力， D {\displaystyle D} 是作用力与支点之间的垂直距离。

则输入力矩等于输出力矩：

杠杆原理表明，当静力平衡时，动力乘以动力臂等于阻力乘以阻力臂：

杠杆的分类

靠着比较动力臂、阻力臂的长度，可以将杠杆分为三类：

动力臂长于阻力臂的杠杆是“省力杠杆”，这可以省力。开瓶器、撬棍等均为省力杠杆。

阻力臂长于动力臂的是“费力杠杆”，这可以费力。大部分剪刀、镊子、筷子、钓鱼竿、火钳、笔等均为费力杠杆。

动力臂和阻力臂长度相等的杠杆是“等臂杠杆”，跷跷板、天平等均为等臂杠杆。

另外一种分类法式依照动力点、阻力点、支点在杠杆的相对位置来分类。

第一类杠杆

第一类杠杆的动力点、阻力点分别在支点的两边。例如，铁撬、剪刀、跷跷板、天平、老虎钳。

第二类杠杆

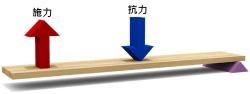
第二类杠杆的动力点、支点分别在阻力点的两边。例如，独轮车、胡桃夹子。这是一种省力杠杆，可以施加较小的力量来移动较重的物体，但是动力的位移较长。

第三类杠杆

第三类杠杆的阻力点、支点分别在动力点的两边。例如，镊子、扫把。这是一种费力杠杆，可以节省动力的位移。

杠杆原理

杠杆是可以绕着支点旋转的硬棒。当外力作用于杠杆内部任意位置时，杠杆的响应是其操作机制；假若外力的作用点是支点，则杠杆不会出现任何响应。

假设杠杆不会耗散或储存能量，则杠杆的输入功率必等于输出功率。当杠杆绕着支点呈匀角速度旋转运动时，离支点越远，则移动速度越快，离支点越近，则移动速度越慢，由于功率等于作用力乘以速度，离支点越远，则作用力越小，离支点越近，则作用力越大。

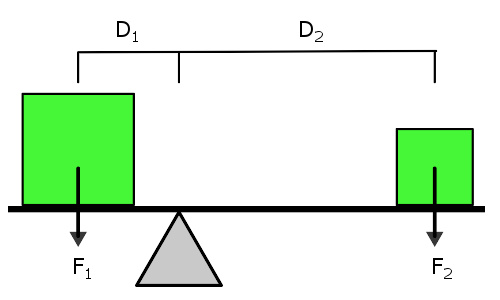
静力平衡的杠杆。

机械利益是阻力与动力之间的比率，或输出力与输入力之间的比率。假设动力臂 D 1 {\displaystyle D_{1}} 、阻力臂 D 2 {\displaystyle D_{2}} 分别为动力点、阻力点与支点之间的距离，动力 F 1 {\displaystyle F_{1}} 、阻力 F 2 {\displaystyle F_{2}} 分别作用于动力点、阻力点。则机械利益 M A {\displaystyle MA} 为

通常在学习杠杆的初级理论时，会聚焦于输入力和输出力由于虚位移而做的虚功。虚位移可以定义为物体的移动速度乘以虚时间。这样定义导致计算的物理量是功率，而不是功。这种方法有一个实在优点：在研究机械工程学或机构学时，功率是主要计算的物理量。使用这种方法来对杠杆做静力分析，就如同对于车子的传动系统，或机械手臂做静力分析，它们的机械利益的计算方式完全一样。

复式杠杆

指甲剪是一种常用的复式杠杆。

复式杠杆（ compound lever ）是一组耦合在一起的杠杆，前一个杠杆的阻力会紧接地成为后一个杠杆的动力。几乎所有的磅秤都会应用到某种复式杠杆机制。其它常见例子包括指甲剪、钢琴键盘。1743年，英国伯明翰发明家 约翰·外艾特 在设计计重秤时，贡献出复式杠杆的点子。他设计的计重秤一共使用了四个杠杆来传输负载。

参阅

连杆组

机构学

单摆

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。