历史

在詹姆斯·麦克斯韦的1864年论文《电磁场的动力学理论》内，麦克斯韦将位移电流与其它已成立的电磁方程合并，因而得到了描述电磁波的波动方程。最令人振奋的是，这方程所描述的波动的波速等于光波的速度。他这样说 ：

理论推导

在真空里，麦克斯韦方程组的四个微分方程为

其中，μ μ -->0{\displaystyle \mu _{0}\,\!}是真空磁导率，ε ε -->0{\displaystyle \varepsilon _{0}\,\!}是真空电容率。

分别取公式(2)、(4)的旋度，

应用一则矢量恒等式（这里，∇ ∇ -->2V{\displaystyle \nabla ^{2}\mathbf {V} }应被理解为对V的每个分量取拉普拉斯算子，即拉普拉斯–德拉姆算子）

其中，V{\displaystyle \mathbf {V} \,\!}是任意矢量函数。

将公式(1)、(3)代入，即可得到亥姆霍兹方程形式的波动方程：

其中，c=c0=1μ μ -->0ε ε -->0=2.99792458× × -->108{\displaystyle c=c_{0}={1 \over {\sqrt {\mu _{0}\varepsilon _{0}}}}=2.99792458\times 10^{8}\,\!} ［米／自由是电磁波传播于自由空间的速度。

齐次的波动方程的协变形式

电磁四维势Aμ μ -->{\displaystyle A^{\mu }\,\!}是由电势ϕ ϕ -->{\displaystyle \phi \,\!}与矢量势A{\displaystyle \mathbf {A} \,\!}共同形成的，定义为

采用洛伦茨规范：

前述那些齐次的波动方程(5)、(6)，可以按照反变形式写为

其中，◻ ◻ -->=∂ ∂ -->ν ν -->∂ ∂ -->ν ν -->=∂ ∂ -->2∂ ∂ -->xν ν -->∂ ∂ -->xν ν -->=1c2∂ ∂ -->2∂ ∂ -->t2− − -->∇ ∇ -->2{\displaystyle \Box =\partial ^{\nu }\partial _{\nu }={\frac {\partial ^{2}}{\partial x_{\nu }\partial x^{\nu }}}={\frac {1}{{c}^{2}}}{\partial ^{2} \over \partial t^{2}}-\nabla ^{2}\,\!}是达朗贝尔算子，又称为四维拉普拉斯算子。

弯曲时空中的齐次的波动方程

齐次的电磁波方程在弯曲时空中需要做两处修正，分别是将偏导数替换为协变导数，以及增加了一项有关时空曲率的项。假设洛伦茨规范在弯曲时空中的推广为

那么，弯曲时空中的齐次的波动方程为

其中，Rα α -->β β -->{\displaystyle {R^{\alpha }}_{\beta }\,\!}是里奇曲率张量。

非齐次的电磁波方程

追根究底，局域化的含时电荷密度和电流密度是电磁波的波源。在有波源的情形下，麦克斯韦方程组可以写成一个非齐次的电磁波方程的形式。正是因为波源的存在，使得偏微分方程变为非齐次。

波动方程的解

在齐次的电磁波方程中，电场和磁场的每一个分量都满足标量波动方程

其中，f{\displaystyle f\,\!}是任意良态函数，

标量波动方程的一般解的形式为

其中，g(k⋅ ⋅ -->r− − -->ω ω -->t){\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}是任意良态函数，r{\displaystyle \mathbf {r} \,\!}是位置矢量，t{\displaystyle t\,\!}是时间，k{\displaystyle \mathbf {波矢 \,\!}是波矢，ω ω -->{\displaystyle \omega \,\!}是角频率。

函数g(k⋅ ⋅ -->r− − -->ω ω -->t){\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}描述一个波动，随着时间的演化，朝着k{\displaystyle \mathbf {k} \,\!}的方向传播于空间。将函数g(k⋅ ⋅ -->r− − -->ω ω -->t){\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}代入标量波动方程(7)，可得到角频率与波数的色散关系：

或者，角频率一定大于零，但波数可以是负值：

正弦波

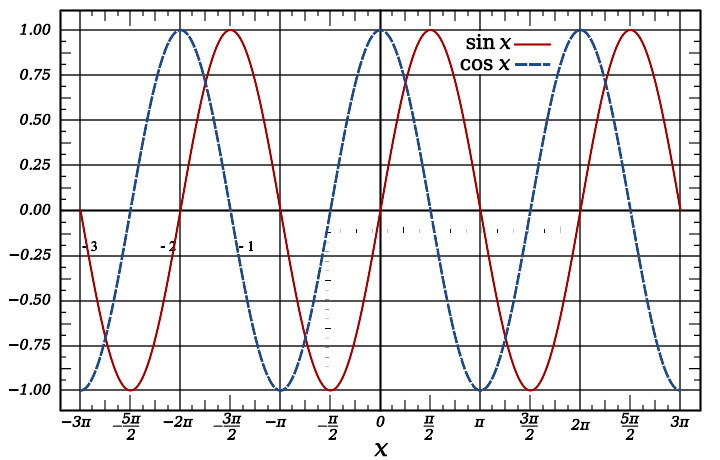
正弦函数和余弦函数的曲线是不同相位的正弦曲线。

假设，函数g{\displaystyle g\,\!}的波形为正弦波：

其中，f0{\displaystyle {f}_{0}\,\!}是实值波幅，ϕ ϕ -->0{\displaystyle \phi _{0}\,\!}是初相位。

根据欧拉公式，

函数f{\displaystyle f\,\!}也可以表达为一个复数的实值部分

以上方加有波浪号的符号来标记复值变数。设定复值函数f~ ~ -->{\displaystyle {\tilde {f}}\,\!}为

其中，f~ ~ -->0=f0eiϕ ϕ -->0{\displaystyle {\tilde {f}}_{0}=f_{0}e^{i\phi _{0}}\,\!}是复值波幅。

那么，

标量波动方程的正弦波解的形式为f~ ~ -->{\displaystyle {\tilde {f}}\,\!}的实值部分。任意涉及实函数f{\displaystyle f\,\!}的线性方程，都可以用复函数f~ ~ -->{\displaystyle {\tilde {f}}\,\!}来代替f{\displaystyle f\,\!}。最后得到的复值答案，只要取实值部分，就可以得到描述实际物理的答案。但是，当遇到非线性方程，必须先转换为实值函数，才能够确保答案的正确性。

由于指数函数比三角函数容易计算，在很多场合，都可以使用这技巧。

线性叠加

任意波动f(r,t){\displaystyle f(\mathbf {r} ,t)\,\!}可以表达为一个无限集合的不同频率的正弦波的线性叠加：

所以，只要能得知单独频率的波动f~ ~ -->0(r,ω ω -->){\displaystyle {\tilde {f}}_{0}(\mathbf {r} ,\omega )\,\!}（单色波）的表达式，就可以求算整个波动f(r,t){\displaystyle f(\mathbf {r} ,t)\,\!}的表达式。

齐次的电磁波方程的解

单色正弦平面波的解

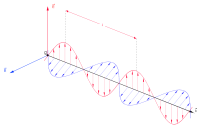
电磁波是横波，电场方向与磁场方向相互垂直，又都垂直于传播方向。

从前面的分析，可以猜到齐次的电磁波方程的单色正弦平面波的解为：

其中，E~ ~ -->0{\displaystyle {\tilde {\mathbf {E} }}_{0}\,\!}、B~ ~ -->0{\displaystyle {\tilde {\mathbf {B} }}_{0}\,\!}分别为复值电场E~ ~ -->{\displaystyle {\tilde {\mathbf {E} }}}和复值磁场B~ ~ -->{\displaystyle {\tilde {\mathbf {B} }}}的复常数振幅矢量。

这两个方程显示出的正弦平面波的传播方向是k{\displaystyle \mathbf {k} \,\!}的方向。由于方程(1)和(3)，

电场和磁场垂直于波矢，波动传播的方向。所以，电磁波是横波。

由于法拉第电磁感应定律方程(2)，

将角频率与波数的色散关系式ω ω -->=ck{\displaystyle \omega =ck\,\!}带入：

所以，电场与磁场相互垂直于对方；磁场的大小等于电场的大小除以光速。

电磁波谱分解

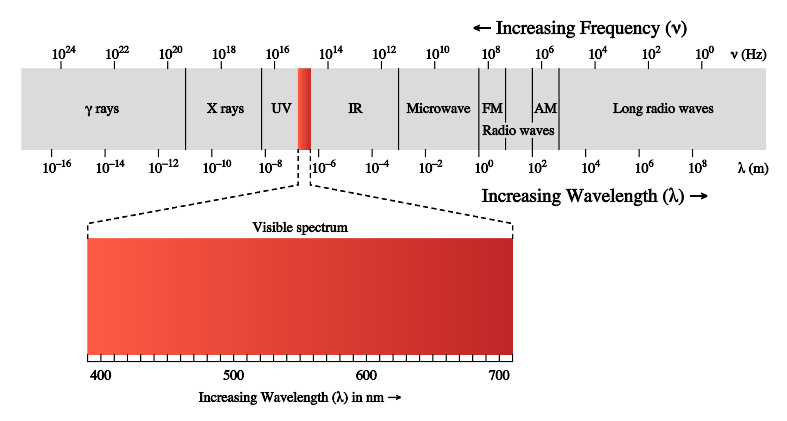
电磁波谱显示出不同种类的电磁波的频率值域和波长值域。可见光谱只占有宽广的电磁波谱的一小部分。

由于麦克斯韦方程组在真空里的线性性质，其解答可以分解为一集合的正弦波。将这集合的正弦波的叠加在一起，又可以形成原本的解答。这是傅里叶变换方法解析微分方程的基础概念。电磁波方程的正弦波解的形式为

波矢与角频率的关系为

其中，λ λ -->{\displaystyle \lambda \,\波长是波长。

按照波长长短，从长波开始，电磁波可以分类为电能、无线电波、微波、红外线、可见光、紫外线、X-射线和伽马射线等等。普通实验使用的光谱仪就足以分析从2奈米到2500 奈米波长的电磁波。使用这种仪器，可以得知物体、气体或甚至恒星的详细物理性质。这是天文物理学的必备仪器。例如，氢原子会发射波长为21.12公分的无线电波。

圆柱对称性解

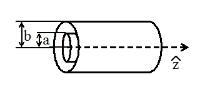
原柱对称形共轴传输线

如图右，思考一条由半径为a{\displaystyle a\,\!}的无穷长的直导线，和半径为b{\displaystyle b\,\!}的无穷长的圆柱导电管，所组成的共轴传输线。假设这传输线与z-轴平行。由于共轴传输线的内部有一条直导线，不是空心的，它可以传输Ez=0{\displaystyle E_{z}=0\,\!}和Bz=0{\displaystyle B_{z}=0\,\!}的电磁横波，采用圆柱坐标(s,ϕ ϕ -->,z){\displaystyle (s,\phi ,z)\,\!}，在传输线的内部空间，电场和磁场分别为

这一组方程显示出电磁波方程的圆柱对称性解的一种形式。

球对称性解

思考一个位于原点的振荡中的磁偶极矩m=m0cos⁡ ⁡ -->(ω ω -->t){\displaystyle m=m_{0}\cos(\omega t)\,\!}。这磁偶极矩会发射出电磁波，从原点往无穷远辐射出去。采用球坐标(r,θ θ -->,ϕ ϕ -->){\displaystyle (r,\theta ,\phi )\,\!}，则在离原点很远的位置r{\displaystyle \mathbf {r} \,\!}，电场和磁场分别为

这是一组满足电磁波方程的球面波方程。

参阅

理论与实验

应用领域

参考文献

Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. 2004. ISBN 0-7167-0810-8. 

Jackson, John D. Classical Electrodynamics (3rd ed.). Wiley. 1998. ISBN 0-471-30932-X. 

Landau, L. D., The Classical Theory of Fields (Course of Theoretical Physics: Volume 2), (Butterworth-Heinemann: Oxford, 1987). ISBN 0-08-018176-7.

Maxwell, James C. A Treatise on Electricity and Magnetism. Dover. 1954. ISBN 0-486-60637-6. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。