-
府院君
由来高丽元宗时期,元朝征服高丽后,下令高丽官名爵号凡是与中原王朝相同的,必须予以更改。高丽尚书省、中书省改成佥议府,枢密院改为密直司,平章事改为赞成事,朕改成孤,诏书改成教书。根据这一命令,高丽王室宗亲和贵族的原有的公、侯、伯、子、男爵位也改为府院大君、府院君、君、元尹和正尹。朝鲜王朝成立后,沿用了这套封爵系统,其间只有在太祖八年“第一次王子之乱”之后一度把爵位改为公、侯、伯,之后又改回原称。但朝鲜王朝时期“府院君”的称号只用于功臣、外戚,并且取消了“府院大君”的封号。王妃所生的嫡子改称为大君,庶子称为君。府院君(功臣)的夫人封为贞敬夫人,外戚则封为府夫人。高丽及朝鲜王朝府院君列表高丽王朝齐安府院大君王淑江阳府院大君王镛咸宁府院大君王维江陵府院大君王祺德兴府院君王益兴府院君王玹庆昌府院君王(忠定王)定昌府院君王瑶(恭让王)泰安府院君李大顺南阳府院君洪奎大宁府院君崔有宁越府院君李信鸡林府院君...
人物百科 | 2017-10-16 -

法国航空
历史1951年,荣军院领导就职1933年10月7日法国航空于法国成立。1948年,法国航空成为法国国营航空公司。1970年,使用波音747型飞机服务长程航线。1983年,法国航空名列世界第四大客运航空公司,也是世界第二大货运航空公司。1988年,法航成为空中客车A320的启动用户,两年后并购因特航空和法国联合航空。1999年2月22日,法国航空股票正式上市。2000年6月22日,法国航空与达美航空、墨西哥国际航空及大韩航空,共同成立‘天合联盟’,之后捷克航空以及意大利航空陆续加入。目前,法国航空为世界重要的航空公司之一。这也是全球除了英国航空之外,第二家拥有协和飞机的航空公司。法航-荷航集团在法国的法律之下成立,而总部则设于巴黎戴高乐国际机场。法国航空-荷兰皇家航空集团是欧洲最大的航空公司,及世界上最大的航空公司之一。法航-荷航集团是“天合联盟”的成员。法国航空公司是“天合联盟”的创始成员...
人物百科 | 2017-10-16 -
过氧化氢
性质纯过氧化氢是淡蓝色的粘稠液体,熔点−0.43°C(31.23°F),沸点150.2°C(302.4°F)。凝固点时固体密度为1.71g/cm,密度随温度升高而减小。它的缔合程度比H2O大,所以它的介电系数和沸点比水高。纯过氧化氢比较稳定,若加热到153°C(307°F)便猛烈的分解为水和氧气。过氧化氢可与水以任意比互溶,因其可以发生微弱电离,所以溶液呈弱酸性。过氧化氢与过量氢氧化钠反应的产物是Na2O2和H2O。而与氢氧化钡反应时产物为过氧化钡。过氧化氢分子为椅型结构,见下图。左图为气态时的结构,右图为固态晶体时的结构:过氧化氢可溶于乙醇、乙醚,不溶于苯。对有机物有很强的氧化作用,一般作为氧化剂使用。催化剂体内的过氧化氢酶(Catalase)可以催化双氧水的分解反应,使其释放出氧气,转化为对有机体无毒的水:发现1818年,L.J.Thenard发现水系无机物、有机物在自动氧化时,或者在...
人物百科 | 2017-10-16 -

康熙帝南巡
过程第一次南巡康熙二十三年(1684年甲子),30岁九月二十八日康熙帝初次南巡启銮。十月初十日,登泰山顶。十月十九日,自徐州府宿迁县启程,是日,驻桃源县,视察黄河北岸各项险要工程,十月二十六日,行至苏州府,十一月二日,在南京谒明太祖陵,亲写祝文,遣官往祭。十一月十八日,到曲阜孔子庙,在大成殿行三跪九叩礼,亲书“万世师表”十二月九日,由京师正阳门回宫。首次南巡共用六十天。第二次南巡康熙二十八年(1689年己巳),35岁正月初二日,康熙帝第二次南巡,临阅河工。正月二十三日,至宿迁县,率领随从大臣及江南总督傅拉塔、河道总督王新命,漕运总督马世济等视察中河。正月二十八日,舟过扬州,民间结彩欢迎。二月十一日抵杭州,民间有“建立碑亭,称颂德意”者,康熙帝谕以有损民力,命停止,并对所有请他多在杭州逗留大臣晓以利弊,概不准奏。二月康熙帝抵达浙江绍兴,祭大禹陵,亲制祭文,书名,行九叩礼,制颂刊石,书额曰“地...
人物百科 | 2017-10-16 -
陪集
范例加法循环群Z4={0,1,2,3}=G有子群H={0,2}(同构于Z2)。H在G中的左陪集为因此存在两种不同的陪集H本身和1+H=3+H。注意每个G中元素或者在H中,或者在1+H中,也即,H∪(1+H)=G,所以H在G中不同的陪集构成G的一个划分。因为Z4是交换群,右陪集和左陪集相同。另一个陪集的例子来自线性空间中。线性空间的向量在向量加法下组成一个阿贝尔群。可以证明原来的线性空间的子空间是这个群的子群。对于给定的线性空间V,子空间W和V中的一个固定向量a,集合被称为“仿射子空间”。它们都是W的陪集。对于欧几里得空间,仿射子空间代表与给定的过原点的直线或平面平行的直线或平面。性质gH=H当且仅当g是H中的元素。一个子群H的两个左(右)陪集要么相同,要么不交——即左(右)陪集的集合构成了群G的一个划分:群中的每个元素属于且仅属于一个左(右)陪集。特别地,单位元只在一个陪集中,即是H自己。...
人物百科 | 2017-10-16 -
至尊法案
至尊法案(ActsofSupremacy)是英国亨利八世于1534年在英国通过的有关皇室至尊的立法。通过此法案,英国国王获得了英国教会最高领袖的地位。该法案标志着英国实行了宗教改革,与罗马天主教会正式分离。在16世纪欧洲宗教改革的大背景下,1529年,都铎王朝的亨利八世以教皇不同意他与王后离婚为由开始与罗马教廷走向决裂;1533年,亨利八世宣布禁止英国教会向罗马教廷缴纳贡金。1534年,英国国会通过了《至尊法案》,宣布英国国王是“英国教会在地上之惟一最高首脑”,从此,英国完全脱离了罗马教廷的控制,成为一个新教国家。《至尊法案》规定:英王为教会首脑;神职人员须效忠英王;信仰得救,《圣经》为惟一标准;否定天主教集一切权力于教皇的教阶制,不承认罗马教皇的绝对权威。与罗马教廷决裂后的英国教会称"安立甘教(AnglicanCommunion)",又称"圣公会(AnglicanChurches)",具...
人物百科 | 2017-10-16 -
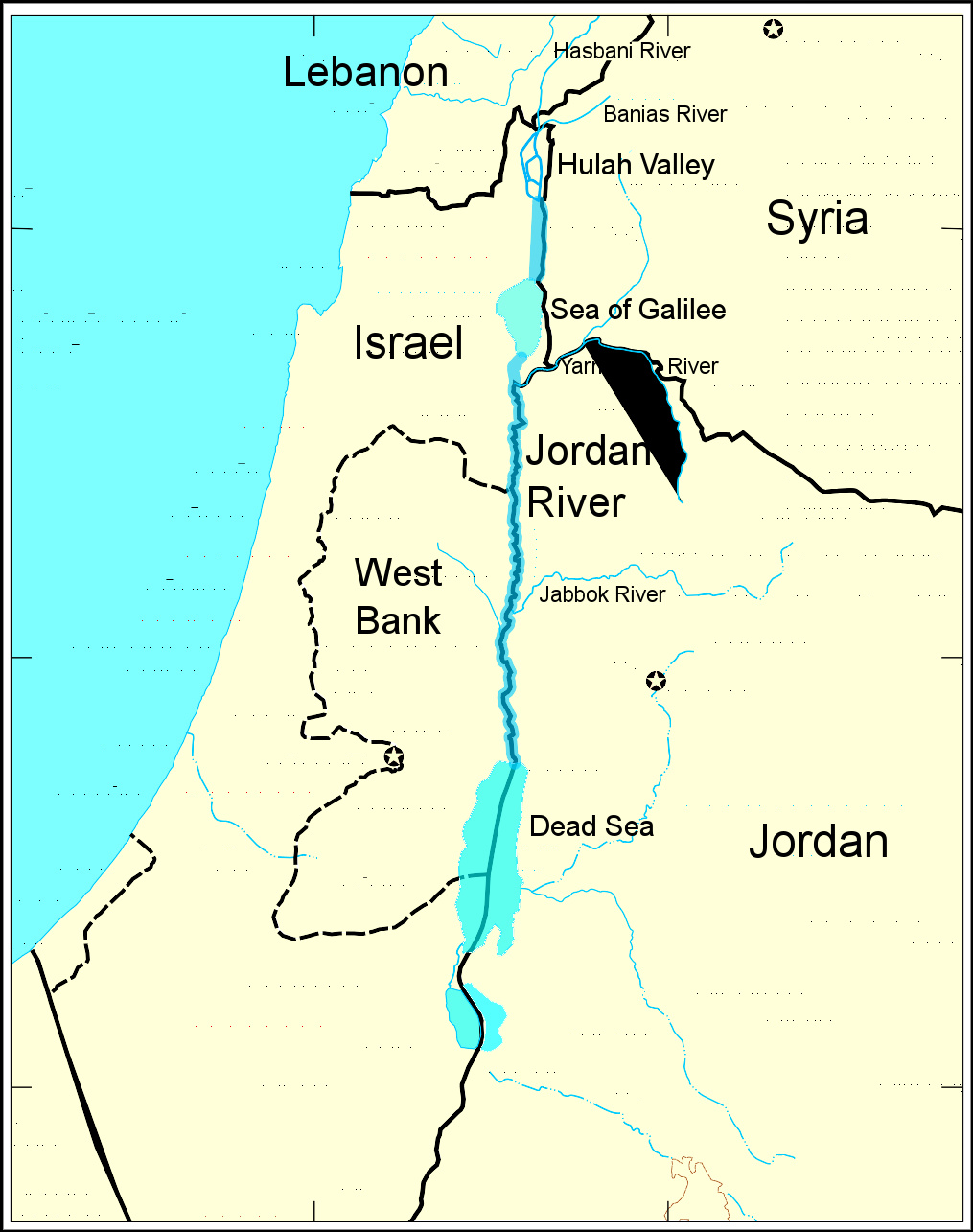
加利利海
词源该湖在现代地图上标为加利利湖或提比利亚湖。它的名字说明它位于加利利地区。现代希伯来语称为YamKinneret(帮助·信息)。可能起源于希伯来语kinnor("
人物百科 | 2017-10-16 -
自同构
定义自同构的精确定义,依赖于“数学对象”的种类,及这对象的“同构”的准确界定。可以定义这些概念的最一般情形,是在数学的一个抽象分支,称为范畴论。范畴论是研究抽象对象和这些对象间的态射。在范畴论中,自同构是一个自同态(即是一个对象到自身的一个态射)而同时为(范畴论所定义的)同构。这是一个很抽象的定义,因为范畴论中,态射不一定是函数,对象不一定是集合。不过在更具象的情形中,对象会是有附加结构的集合,而态射会是保持这种结构的函数。例如在抽象代数中,一个数学对象是代数结构,如群、环、向量空间等。一个同构就是双射的同态(同态按代数结构而定,例如群同态、环同态、线性算子)。恒等态射(恒等映射)在某些情况称为平凡自同构。相对地,其他(非恒等)自同构称为非平凡自同构。自同构群如果一个对象X的自同构组成一集合(而不是一个真类)那么这些自同构以态射复合运算组成一个群。这个群称为X的自同构群。可以直接检查这的确...
人物百科 | 2017-10-16 -
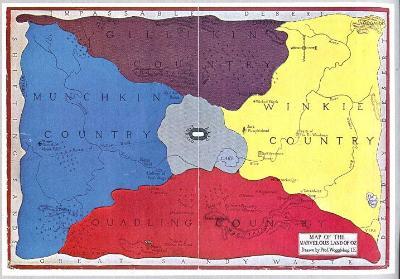
奥兹国
地理奥兹国奥兹仙境四面被沙漠环绕,将奥兹居民与世隔绝。国土大致为长方形,以对角线切割成四个主要国家。西边是蛮支金国(又译为曼奇津国,MunchkinCountry),东边是闻绮斯国(又译为温基国,WinkieCountry),北边是吉利金国(又译为吉力金国,GillikinCountry),南边是奎德林国(QuadlingCountry),中央交界处则是奥兹国的首都翡翠城(EmeraldCity)。1914年出版的《奥兹国的机器人》(又译为《欧兹的机器人》,Tik-TokofOz)中,奥兹地图将西方画在右边,东方在左边,北方仍在上,南方在下。历史奥兹国最早出现在1900年由李曼·法兰克·鲍姆所著的童话《绿野仙踪》中,书中的奥兹国历史应有上百年了。教育在首都翡翠城中的皇家体育学院是奥兹国中最具盛名的学习殿堂,学生服用药丸来学习阅读、写作和算数,其它大部分的时间安排体育课程。
人物百科 | 2017-10-16 -
留里克王朝
历史留里克王朝的实际始祖为基辅大公伊戈尔·留里科维奇,其后代成为基辅罗斯的王公家族。按照传统说法,伊戈尔为半传说式的人物、诺夫哥罗德的第一位王公留里克之子,王朝的名字即源于留里克之名。据编年史记载,留里克、西涅乌斯、特鲁沃尔系兄弟三人,是来自北欧的瓦良格人(瑞典系的诺曼人)的领袖。留里克领导瓦良格人来到斯拉夫人的居住地。看来,他首先成为了拉多加的统治者。编年史说,留里克在诺夫哥罗德人的请求下,成为该城的大公,留里克王朝遂此奠基。然而,按照多数现代研究者的看法,他用武力夺取诺夫哥罗德的可能性显然更大,因为史料提到在留里克取得公位之后不久即发生过一次起义。留里克的继任者奥列格征服基辅,使那里成为几个世纪里罗斯的政治中心。从伊戈尔开始,古罗斯国家无论是基辅大公国还是封建分裂时各大小公国的统治者都是留里克王朝的成员。在封建分裂时期,留里克王朝亦分为几个支系,其中最主要的是莫诺马霍维奇支系(基辅大公...
人物百科 | 2017-10-16




